How do we know that atoms really exist?

All things are made of atoms

If you had never heard of atoms or molecules, you wouldn’t have much reason to think you couldn’t take a block of wood or metal or what have you, chop it in half, chop one of the resulting pieces in half again, and so on and so forth ad infinitum.  Maybe you’d have to get a sharper knife at some point, but the idea that you’d get to a point where you could no longer chop the block in half, even with an infinitely sharp knife, would probably seem a little arbitrary.  And yet, the atomic theory is so fundamental to our understanding of the world that we tend to overlook how revolutionary and controversial it’s been throughout history.  Richard Feynman, the 1965 winner of the Nobel Prize in Physics, once remarked:

If, in some cataclysm, all of scientific knowledge were to be destroyed, and only one sentence passed on to the next generations of creatures, what statement would contain the most information in the fewest words? I believe it is the atomic hypothesis (or the atomic fact, or whatever you wish to call it) that all things are made of atoms—little particles that move around in perpetual motion, attracting each other when they are a little distance apart, but repelling upon being squeezed into one another. In that one sentence, you will see, there is an enormous amount of information about the world, if just a little imagination and thinking are applied…

So how is it that anyone came up with such a crazy idea in the first place?  And how were we ever able to figure out that atoms actually exist?

The Rise of Atomism

The idea that the world might be made up of indivisible parts is typically attributed to  Democritus, an early Greek philosopher.  Democritus’ atomic hypothesis arose in response to the philosophical problem of motion, posed by Parmenides and in a different form by Zeno.  Both argued that motion was an illusion.  Zeno’s argument, which may be a little more familiar to the modern reader, is as follows:

1) For something to move from point A to point Z, it has to first move to a point halfway between the two (call it point B).

2) For something to move from point B to point Z, it has to move to a point halfway between these two points (call it point C).

3) This argument can be continued ad infinitum, but since any motion takes time, and this motion is made up of an infinite number of steps, it should take an infinite amount of time for any motion to occur at all.  Therefore, motion is an illusion.

(For a solution to Zeno’s paradox, see: How do we know that 1/2 + 1/4 + 1/8 + … = 1?)

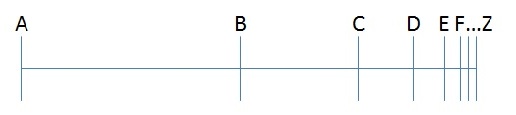
Parmenides’ argument, which is a little more of a brain-bender, is as follows:

1) You can’t have two things at the same place at the same time (note that the ancient Greeks considered air and water to be “things”).

2) For motion to occur, something would have to move into a place where there was nothing (this follows from assumption 1 above).

3) But you can’t have a place where there is nothing, because if nothing existed, then it would be something.  Therefore, there can’t be nothing (modern translators usually translate “nothing” as “the Void”).

4) But if there’s no such thing as nothing, then there’s nowhere for something that’s moving to move into.  This means that motion must be an illusion.

The above arguments may seem like tortured reasoning to us in the 21^st century, but apparently they were quite convincing to philosophers in the 4^th century BC, and Democritus sought to answer them.  To do this, he rejected Parmenides’ account of “nothing” or “the Void.”  He argued that something did move into nothing, but that something like air or water, instead of being an immutable, single, continuous entity, was actually made up of tiny indivisible pieces that were separated by Void and could rearrange themselves in space.  Thus, things could in fact move through air or water.  This is actually not far off from our modern view of atomic theory.  Conveniently, by postulating that everything was made up of indivisible units, he was able to answer Zeno by allowing that motion could only occur in indivisible units, and so you’d never have the infinite divisibility problem that characterizes Zeno’s paradox.  Democritus’ atomism hence offered an elegant solution to the problems posed by earlier philosophers.  So why did it fall out of favor?

Aristotle and the Church’s Rejection of Atoms

The figure most associated with killing the atomic theory is Aristotle.  Historians have argued to what extent Aristotle was directly responsible–some suggest that a passage from his Physics proves that he advocated indivisible units of matter–but what is certain is his vigorous rejection of Democritus’ theory.  In his treatise On the Generation and Corruption, Aristotle enumerates many arguments for why Democritus’ atomism leads to logical absurdities.  All of these arguments hinge on the premise that atoms were not only indivisible in their form, but also indivisible–and therefore unchangeable–in all their properties.  For example, an atom moving at a certain speed will always move at that speed, because that speed is an indivisible and therefore unchangeable property of the atom.  Whether or not the handful of cryptic passages in Aristotle’s Physics signify a sympathetic softening toward the existence of atoms, it is clear that Aristotle thought Democritus’ theory of atoms was unacceptably inconsistent.  Aristotle’s authority was probably sufficient to doom the atomic theory for several hundred years.  But to add insult to injury, the next philosophers to pick up the cause of atomism were the Epicureans.  Their value system famously identifies pleasure as the highest attainable good and asserts that the gods are nonparticipating observers in earthly affairs.  Later, the central tenets of Epicureanism would be seen by early Church fathers as promoting atheism and pagan bacchanalia.  And anyone purporting to be an atomist during this period had to be very careful, lest he be saddled with the label “Epicurean.”

Corpuscules and the Birth of Modern Atomic Theory

In the seventeenth century, Robert Boyle and Isaac Newton began advocating a brand of atomic theory known now as corpuscularianism.  This renewed interest in atoms came out of the belief that, just as a complex machine is best understood by understanding the workings of its parts, so too can nature be better understood by examining its constituent parts.  However, a truly scientific approach to atoms would have to wait another 150 years until John Dalton began studying how different gases were absorbed into water.

Dalton’s key observation was that many gases could go into and out of water without reacting with the water chemically.  As an example, look at the picture above.  The water has been boiled briefly to remove dissolved air.  After letting the water cool completely, you can put a tube filled with air upside down into the water.  You will observe after several hours that the water level rises in the tube as the water begins to absorb the air in the tube.  Dalton noticed that by heating the water or by applying suction to it, he could pull the same amount of air out of the water that he put in. He reasoned that this happens because tiny particles of air were escaping down into the water.  In other words, water absorbs gases by mechanical means, rather than chemical means, and this happens when gas molecules disperse themselves among water molecules.

Dalton even went so far as to calculate the relative masses of the different atoms.  He did this by comparing the masses of the elements required to give certain compounds.  To take a modern example, you can make 100 grams of water by reacting 11.1 grams of hydrogen with 88.9 grams of oxygen.  A ratio of 11.1:88.9 is equal to a ratio of 1:8.  This means there is 8 times as much oxygen as there is hydrogen by weight.  Dalton erroneously assumed that the chemical formula for water was HO when he did this calculation, so he would have asserted that oxygen atoms were 8 times heavier than hydrogen atoms.  (He actually asserted that oxygen atoms were 7 times heavier than hydrogen atoms, because of the inaccuracy of his experiments).  However, if we take into account that the formula for water is actually H₂O, we get that oxygen is 16 times heavier than water, which agrees with the modern value on the periodic table.

Avogadro and How We Know that Water is H₂O

We have described above how Dalton noted that the weights of compounds created in chemical reactions were made up of whole number ratios of the weights of their elements.  In 1808, Joseph Gay-Lussac published observations showing that the volumes of gaseous elements also combine to give simple whole number ratios.  He showed, for example, that 2 volumes of hydrogen and 1 volume of oxygen give 2 volumes of water.  He showed similar simple ratios for ammonia (3 vol. hydrogen to 1 vol. nitrogen), carbon dioxide (1 vol. oxygen to 2 vol. carbon monoxide), and a host of other compounds.  In 1811, Amedeo Avogadro realized that the only way to view these data consistently was to assume that equal volumes of different gases have equal numbers of particles.  In other words, one liter of oxygen gas contains the same number of molecules as one liter of hydrogen gas.  Avogadro’s work was not acknowledged as valid until nearly 50 years later, by which time Avogadro himself had died.  Nevertheless, “Avogadro’s law” as it’s known today is the reason we know that the formula for water is H₂O, and not HO.

The Karlsruhe Congress

In September of 1860, a collection of the most distinguished chemists in the world convened in Karlsruhe to discuss what to do about the burgeoning “new chemistry,” that seemed infested with the idea of atoms and molecules.  On the one hand, scientists like Stanislao Cannizzaro argued outright for Avogadro’s hypothesis (and the modern view), that elements were made up of real physical atoms, which themselves could be combined into molecules.  On the other hand, scientists such as August Kekule argued that, while the atomic theory was a useful framework to interpret the results of chemical experiments, one could not use the results of chemistry to say that physical atoms actually exist.  The “chemical” atom, for Kekule, was a statement that certain elements could only be combined in fixed quantities, whereas the “physical” atom was a statement that the world was actually made up of tiny, indivisible pieces of matter.  And other scientists such as Marcellin Berthelot argued that one should not even use the word “atom” in chemistry, preferring to use atom-agnostic language like “equivalent.”  (So water was “2 equivalents of hydrogen, 1 equivalent of oxygen,” instead of, “2 atoms of hydrogen, 1 atom of oxygen.”)

A further roadblock in acceptance of the theory was brought up by Berthelot and Charles de Marignac and discussed by Charles Adolphe Wurtz.  In the course of their studies on atoms and molecules, many scientists had found that some elements seemed to be paired up with themselves; for example, hydrogen, oxygen, and chlorine all seemed to have the formula H₂, O₂, and Cl₂.  But since the whole concept of an atom was that it was indivisible, it didn’t make much sense to some scientists that many of these indivisible elements like hydrogen were in fact divisible and made up of multiple atoms.  The chemists left the Karlsruhe Congress without really having resolved anything, but Cannizzaro’s work, including his widely distributing a review of Avogadro’s hypothesis, would continue to spur on vigorous debate for at least the next 30 years.

Attack of the Physicists

At the time of the Karlsruhe Congress, physicists and chemists were largely ignorant of each other’s work.  Daniel Bernoulli had proposed in 1738 that gases were made up of an enormous number of small corpuscles bouncing around in every direction.  Their collisions with each other and with everything else were the microscopic cause of what we observe as pressure, and the speed of these collisions were perceived by us as heat or temperature.  His ideas in this direction were largely ignored, and it wasn’t until the 1850’s, when August Krönig and Rudolph Clausius developed the physics behind this model, that atomic theory began to be taken seriously by physicists.  Clausius examined data from experiments on how heat flows into and out of gases and noticed that many of the results could be explained if gas molecules had internal structure; in other words, molecules were made of atoms that moved like weights on a spring.  His model was taken up by James Clerk Maxwell and later by Ludwig Boltzmann, and in 1873, Maxwell published a comprehensive review of molecular and atomic theory in Nature.

His paper tied together, for the first time, many separate experimental results—Electrolysis: water could be split into hydrogen and oxygen gas if an external voltage was applied; Spectroscopy: Robert Bunsen and others had given  preliminary evidence which strengthened the notion, first rigorously examined by Clausius, that certain molecules may have internal structure; and Diffusion: the diffusion of ammonia gas into hydrochloric gas to form a solid product, ammonium chloride, is a powerful visual demonstration of the motion of molecules. Maxwell also gave what was perhaps the clearest definition of a molecule up to that point:

A molecule of a substance is a small body such that if, on the one hand, a number of similar molecules were assembled together they would form a mass of that substance, while on the other hand, if any portion of this molecule were removed, it would no longer be able, along with an assemblage of other molecules similarly treated, to make up a mass of the original substance.

Brown, Einstein, and a Final Answer to the Atomic Question

In 1827, a Scottish botanist named Robert Brown was observing pollen suspended in water under his microscope when he noticed that smaller fragments of the pollen seemed to be exhibiting a random motion, as if they were bouncing around by some unseen force.  He noticed that tiny grains of minerals exhibited the same motion, so it could not be attributed solely to living matter.  His work was noted as a mere curiosity to physicists until Georges Gouy noted in 1888 that this “Brownian motion” could not be explained in terms of thermal convection.  Observers had noted the similarity of Brownian motion to the motion of dust particles in a sunbeam, which move on small air currents.  However, in the case of Brownian motion, Gouy observed that even two particles very close together in a liquid execute motions that are completely uncorrelated.  If small currents were causing the motion, the particles would not move independently of one another.  Gouy hypothesized that the motion was instead caused by the ceaseless agitation from invisible molecules of the underlying fluid.

However, the mathematical framework to properly analyze this type of statistical motion did not yet exist.  This framework would be developed independently several times over the next few decades, but the first person to give a precise predictive model for Brownian motion was Albert Einstein.  The starting point for Einstein’s model of Brownian motion was to consider a large sphere (the pollen particle) submerged amongst a multitude of much smaller spheres (water molecules), each moving in a random direction with a random velocity and colliding like billiard balls.  In this view, many small spheres are colliding with the large sphere from all directions, causing it to bounce around.  Einstein wanted to quantify this by calculating, on average, how far a Brownian particle would travel from its initial location in a certain time period.  He reasoned that this had to be related to the phenomenon of diffusion that Maxwell had mentioned in his 1873 Nature paper.  If he could relate the size of the pollen particle to how far it wandered, he would be able to calculate roughly how many water molecules were hitting it, and from this, their masses.

To appreciate Einstein’s insight, you have to realize that it isn’t enough just to average out all the collisions of the water molecules with the pollen grain.  To better visualize this, let’s pretend that the pollen grain can only move in a straight line, either backwards (negative direction) or forwards (positive direciton).  But in a completely random system, the pollen is equally likely to get hit from either side, meaning the average is zero motion.  But Einstein realized that if you square the motion after each collision, all the numbers become positive and you can calculate how far the pollen grain is likely to “wander” in any direction from its initial location. This statistical process was not completely new, but until Einstein, it had only been applied to large groups of particles.  Einstein was the first to attempt to apply it to a single particle and to use that formalism to make observable predictions.  It only remained for an experimental scientist to do the observations.

That scientist was Jean Baptiste Perrin in 1909.  He found that if you dissolve a natural pigment known as gamboge into methyl alcohol and then add a large quantity of water, you can produce tiny latex particles about 0.2 microns (0.0002 millimeters) in diameter.  He used a camera lucida, a type of projector, to draw the microscope image onto a grid of paper, which he could use to track the motions of the particles over time.  Perrin thus was able to fully vindicate Einstein’s theory, remarking: “It is simply a question of patience and time; nothing limits a priori the accuracy of the results, and the mass of the atom can be obtained, if desired, with the same precision as the mass of the Earth.”

Perrin’s results marked the final victory for atomic theory, and an explosion of science proceeded with atoms at the center of it all.  Quantum mechanics, modern chemistry, particle physics were all built upon the foundation of the atom, and the atomic theory ushered in the century of wildly rapid scientific progress that we have witnessed since.  In the past few years, our technology has advanced to the point where we can produce pictures, like the one at the top of this post, of individual atoms.  In that one image, we see directly a fundamental fact of our universe that philosophers, physicists, chemists, and even a botanist have struggled for over 2,500 years to understand.  And that’s how we know that atoms really exist.

References

• R. P. Feynman, Six Easy Pieces, p. 4.
• S. Berryman, “Ancient Atomism,” Stanford Encyclopedia of Philosophy. http://plato.stanford.edu/entries/atomism-ancient/#1
• Aristotle, trans. H. H. Joachim, “On the Generation and Corruption.” Retrieved from http://ebooks.adelaide.edu.au/a/aristotle/corruption/index.html
• A. G. M. van Melsen, From Atomos to Atom, Dover, pp. 41-43.
• P. Alexander, Ideas, Qualities and Corpuscles: Locke and Boyle on the External World.  Cambridge University Press, pp. 60-63.
• J. Dalton, “On the Absorption of Gases by Water and Other Liquids,” Memoirs of the Literary and Philosophical Society of Manchester, Second Series, 1, 271-87 (1805).
• A. Avogadro, “Essay on a Manner of Determining the Relative Masses of the Elementary Molecules of Bodies, and the Proportions in Which They Enter into These Compounds,” Journal de Physique 73, 58-76 (1811).
• J. L. Gay-Lussac, “Memoir on the Combination of Gaseous Substances with Each Other,” Mémoires de la Société d’Arcueil 2, 207 (1809).
• M. J. Nye, The Question of the Atom, Los Angeles: Tomash, 1984.
• J. C. Maxwell, “Molecules,” Nature 8, 437-41 (1873).
• R. Brown, The miscellaneous botanical works of Robert Brown: Vol. 1. (Ed. J. J. Bennett). R. Hardwicke: London, 1866.
• A. Einstein; R. Fürth, “On the Movement of Small Particles Suspended in a Stationary Liquid Demanded by the Molecular-Kinetic Theory of Heat” trans. A. D. Cowper (1926, orig. in German 1905). Investigations on the theory of the Brownian motion, Dover Publications.
• J. Perrin, “Brownian Motion and Molecular Reality,” Annales de Chimie et de Physique 18, 1-114 (1909), trans. F. Soddy (1910). London: Taylor and Francis.
• And a big thanks to Carmen Giunta, who compiled a list of classic chemistry papers, many of which were used in this entry.  His website is here:  http://web.lemoyne.edu/~giunta/papers.html